Introduction to the CKKS encryption scheme

Scope
We continue our blog series on Fully Homomorphic Encryption (FHE) and its applications. In the previous article, we introduce the readers to the levelled Brakerski-Gentry-Vaikuntanathan BGV scheme [BGV14]. Here, we present the 3rd article in this series and talk about the Cheon-Kim-Kim-Song FHE scheme [CKKS17]. Note: this article is also available as a PDF Document .

CKKS, a.k.a. Homomorphic Encryption for Arithmetic of Approximate Numbers (HEAAN), was proposed to offer homomorphic computation on real numbers. The main idea is to consider the noise, a.k.a. error $e$, which is introduced in Ring-Learning with Errors (Ring-LWE) based FHE schemes for security purposes, as part of the message $\mu$ (which we call here payload) we want to encrypt. The payload and the noise are combined to generate the plaintext ($\mu+e$) that we encrypt.

Thus, the encryption procedure takes in $(\mu + e)$ as input and generates a ciphertext that encrypts an approximate value of our payload. The rationale behind this is that if the noise is much lower in magnitude compared to the payload, it might not have a noticeable effect on the payload or results of computing over the payload. In fact, even in the normal context without considering encryption, computers use fixed-point or floating-point representations to handle real data. Some real data cannot be represented exactly using these systems, and all we can do is to approximate them with a predefined precision via standard truncation or rounding procedures. This approximation results in errors that can accumulate and expand during computation. But for most realistic scenarios, the errors are not much significant and the final result is therefore satisfactory. Therefore, we sort of can think of the RLWE error in the encrypted domain as truncation or rounding error in the clear domain.

Similar to other FHE schemes, in CKKS, as we compute on ciphertexts, the plaintext (which includes the payload and the error) magnitude grows. If we add two ciphertexts, the growth is limited, but, if we multiply them, the growth is rather higher. Take an example $\mu_1 = 2.75$ and $\mu_2 = 3.17$. The product of $\mu_1 \cdot \mu_2 = 8.7175$. Clearly, the number of digits in the product has doubled. Assuming we fixed the precision at two decimal digits, the product can be scaled down by 100 to produce $\hat{\mu}^{\times} = 8.71$ (if we use truncation) or $\tilde{\mu}^{\times} = 8.72$ (if we use rounding). Generally speaking, both values are good approximates of the exact value of the product adequate for most realistic scenarios. In this rather simplified example the precision is only 2 decimal digits, in IEEE-754 single- and double-precision standards, the precision is fixed at 7 and 15 digits, respectively, providing much more accurate results.

While scaling down is a trivial procedure in the clear domain, it is generally quite expensive in the encrypted domain. Earlier solutions suggest approximating the rounding function as a polynomial for extracting and removing lower digits of encrypted values [HS15, CH18]. We know that FHE is ideally well suited for evaluating polynomials on encrypted data making this approach sensible and straightforward to implement. Unfortunately, this approach is computationally expensive and may not be practical for general scenarios due to the large degree of these polynomials. This, however, has entirely changed after CKKS.

At the heart of the CKKS scheme is a mechanism, called $\textsf{RESCALE}$, that is used to reduce the magnitude of the plaintext (payload and noise). This procedure can be used to simulate the truncation procedure very efficiently. CKKS employed the commonly known FHE procedure $\textsf{MODSWITCH}$ (short for modulus switching) that is mostly used in the BGV scheme, as described in our previous article, to implement this rescaling functionality. In fact, one shall soon notice the great similarity between the two schemes.

CKKS decryption generates an approximate value of the payload $(\mu + e)$ with adequate precision. Only if the magnitude of the error is much smaller than that of the payload, this would be acceptable. Fortunately, this is generally the case - given that the scheme is parameterized wisely - since the noise can be controlled as will be described later.

CKKS $\textsf{RESCALE}$ provides a natural way to compute on encrypted real numbers unlike other FHE schemes (such as Fan-Vercauteren (FV) [FV12] or Brakerski-Gentry-Vaikuntanathan (BGV) [BGV14]) that compute naturally on integers. It should be remarked that one can perform homomorphic computation on encrypted real numbers using BFV and BGV, but that requires sophisticated (and generally inefficient) encoding procedures [CSVW16]. Moreover, scaling down the results during computation is rather difficult.

Figure 1: Ciphertext structure in the BGV and CKKS schemes. MSB stands for most significant bit. Adapted from [CKKS17].

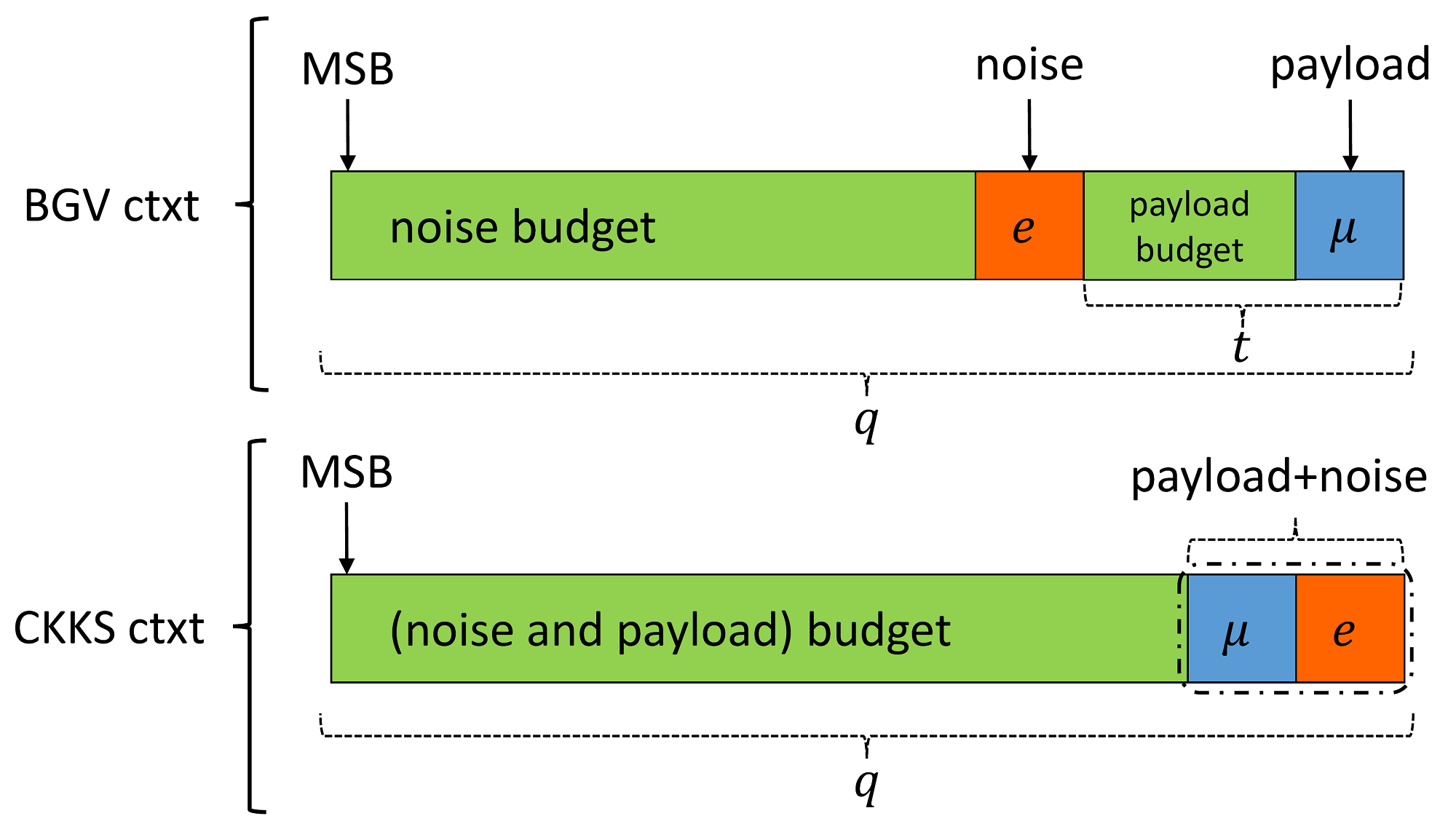
To get an idea of how CKKS works, Figure 1 can be of aid. The figure shows the ciphertext structure of BGV and CKKS. The ciphertext in BGV and CKKS (and even for BFV) is typically a pair of polynomials. One polynomial contains the payload information while the other is used for decryption. The coefficients of these polynomials are bounded by the integer $q$, known as the ciphertext coefficient modulus, that is, they can take any value between $0$ and $q-1$. Without loss of generality and for ease of illustration, suppose the polynomials are of degree $0$. In Figure 1, we show the polynomial that contains the payload information in both BGV and CKKS schemes.

Let's first study the BGV ciphertext structure. It is useful to keep this analogy in mind and think of the ciphertext as a bounded space. The green-colored areas are the open space an entity may reside in. The space in our ciphertext is bounded by the value of $q$. Two main entities are of particular interest, the payload $\mu$ and the noise $e$. In BGV, these two components are separated and should not interact at any stage of the computation, otherwise, the payload will be lost. The separation is simply done by scaling the noise component $e$ by $t$ during encryption. This will shift the error to the left by $t$ as depicted in Figure 1 (BGV ctxt). The payload can freely move in the space bounded by $t$, i.e., taking any value between $0$ and $t-1$. This should be maintained during homomorphic computation as well. The noise component $e$ is free to move in the space bounded by $t$ to $q-1$ (actually less than that but let's not get into details to keep the illustration simple). As long as the error or the payload resides in their respective space, decryption works and the expected payload or computed results can be retained with zero loss in precision.

The ciphertext in the CKKS scheme has a slightly different structure. Firstly, the two main components $\mu$ and $e$ are combined to form one single entity. The noise is part of the payload. As a matter of fact, there is no way of separating these two components (to their exact values) after encryption. This larger entity can now move freely in the space bounded by $q$. One might legitimately wonder that combining $\mu$ and $e$ might distort or corrupt the payload, especially if the payload is of small magnitude (same order of $e$). This is a valid concern and addressing it is quite simple, CKKS scales the payload by a parameter, known as the scale factor $\Delta$. This will move the most significant bits of the payload to the left farther from $e$. The assumption is that the least significant bits of $\mu$, which will be distorted by adding $e$, are not of much significance which happens to be true in practice. To help you see why this is the case, let's work out the following example.

Example 1.1. Let $\mu = \pi = 3.14159265358979323846 \ldots$, $e = 20$ and $\Delta = 10^6$. Assume we are using truncation for trimming down the least significant digits after scaling. We have: $\Delta \cdot \mu + e = 3141592+20 = 3141612$, which is still a good approximation of the scaled payload. If we want to retrieve the original payload, we can simply divide by the scale factor. Thus we have, $3141612/10^6=3.141612$ which is, generally speaking, still a good approximation of $\pi$. We could get a better approximation if we used a larger $\Delta$.

Before we delve further into describing CKKS primitives more concretely, it would be good to brush up on fixed-point arithmetic since what CKKS does, is actually simulating fixed-point arithmetic in the encrypted domain. We refer the reader to Appendix A for an overview of fixed-point arithmetic.

In CKKS, the plaintext and ciphertext spaces are almost the same. They include elements of the polynomial ring $R_q = \Z_q[x]/f(x)$, where $q$ is an integer called the coefficient modulus and $f(x)$ is a polynomial known as the polynomial modulus. Elements of $R_q$ are polynomials with integer coefficients bounded by $q$. Their degrees are also bounded by the degree of $f(x)$. The most common choice of $f(x)$ in the literature is $f(x)=x^n+1$ with $n$ (known as the ring dimension) being a power of 2 number. The difference between CKKS plaintext and ciphertext instances is the number of ring elements they contain. An instance of CKKS plaintext includes one ring element (polynomial) whereas an instance of CKKS ciphertext includes at least 2 ring elements.

The previous paragraph might be thought of as contradicting to what CKKS was originally proposed for, i.e., computing on encrypted real numbers since the plaintext is a polynomial with integer coefficients. The key idea to note is that, CKKS proposes new encoding and decoding ($\textsf{codec}$) techniques, that will be described later, to map a vector of real numbers (more precisely complex numbers) into the plaintext space and vice versa. As we mentioned previously, CKKS simulates fixed-point arithmetic operations which can be done on integral operands via integer operations.

Another main contribution of the CKKS work [CKKS17] is a new $\textsf{codec}$ method that maps a vector of complex numbers into a single plaintext object and vice versa. Encoding works as follows, given an $\frac{n}{2}$-vector of complex numbers $z \in \mathbb{C}^{\frac{n}{2}}$, return a single plaintext element $a \in R$. Decoding does reverse encoding by taking a plaintext element and returning a vector of complex numbers. This is done using Equation \ref{eq:ckks:codec}. The map $\pi$ is the complex canonical embedding which is a variant of the Fourier transform. \begin{equation}\label{eq:ckks:codec} \begin{split} \textsf{ENCODE}(z, \Delta) &= \lfloor \Delta \cdot \pi^{-1}(z) \rceil\\ \textsf{DECODE}(a, \Delta) &= \pi(\frac{1}{\Delta}\cdot a) \end{split} \end{equation}

It should be clear by now the connection between the CKKS $\textsf{codec}$ scheme and fixed-point representation. While we encode the input payload, scaling is done by multiplying by $\Delta$ and removal of least significant fractional parts is done via rounding. In decoding, we reverse this procedure. Multiplying by $\Delta$ and rounding in encoding and division by $\Delta$ in decoding are similar to what we did in fixed-point encoding in Equation \ref{eq:conv:real:to:fixed}.

So far, we came across the parameters $n$, $q$ and $\Delta$. CKKS uses the following additional Ring-LWE-specific distributions in its instantiation:

• $R_2$: is the key distribution used to uniformly sample polynomials with integer coefficients in $\{-1,0,1\}$.
• $\mathcal{X}$: is the error distribution defined as a discrete Gaussian distribution with parameters $\mu$ and $\sigma$ over $R$ bounded by some integer $\beta$. According to the current version of the homomorphic encryption standard [ACC+18], $(\mu, \sigma, \beta)$ are set as $(0, \frac{8}{\sqrt{2\pi}}\approx 3.2, \lfloor 6\cdot \sigma \rceil = 19)$.
• $R_q$: is a uniform random distribution over $R_q$.

Regarding the choice of the parameters $(q, n)$, the same discussion we made in the BFV article also applies here. One thing to note is that $q$ should be large enough to support the desired multiplicative depth of the computed circuit. Given the value of $q$ is fixed, $n$ is determined to provide a sufficient security level. For this purpose, an RLWE hardness estimator can be used [APS15].

We remark that, unlike the BFV scheme we described in our first article, CKKS is a scale-variant scheme. This means that at each level, there is a different coefficient modulus. Remember, as we perform homomorphic multiplication, the ciphertext is scaled down by $\Delta$. This results in reducing the size of $q$ by $\Delta$ and we end up in a ring whose coefficient modulus is $q'=\frac{q}{\Delta}$. Hence, hereafter, we refer to the coefficient modulus at level $l$ by $q_l$, where $1 \leq l \leq L$, and $L$ is the level of a freshly encrypted ciphertext. Therefore, our ciphertext coefficients are related to each other by: \begin{equation} q_L > q_{L-1} > \ldots > q_1 \end{equation}

This procedure is quite similar to the Key Generation procedure in BFV. We sample the secret key $\textsf{SK}$ an element from $R_2$, i.e., a polynomial of degree $n$ with coefficients in $\{-1,0,+1\}$. The public key $\textsf{PK}$ is a pair of polynomials $(\textsf{PK}_1, \textsf{PK}_2)$ calculated as follows: \begin{align} \textsf{PK}_1 &= [-a\cdot \textsf{SK} + e]_{q_L} \\ \textsf{PK}_2 &= a \xleftarrow{\mathcal{U}} R_{q_L} \end{align} Thus, $a$ is a random polynomial sampled uniformly from $R_{q_L}$, and $e$ is a random error polynomial sampled from $\mathcal{X}$. Recall that the notation $[\cdot]_{q_L}$ implies that polynomial arithmetic should be done modulo $q_L$. Note that as $\textsf{PK}_2$ is in $\R_{q_L}$, polynomial arithmetic should also be performed modulo the ring polynomial modulus $(x^n+1)$.

To encrypt a plaintext message $\textsf{M}$ in $R$ (which is an encoding of the input payload vector). We generate 3 small random polynomials $u$ from $R_2$ and $e_1$ and $e_2$ from $\mathcal{X}$ and return the ciphertext $\textsf{C} = (\textsf{C}_1,\textsf{C}_2)$ in $R_{q_l}^2$ as follows: \begin{align}\label{eq:encrypt} \textsf{C}_1 &= [\textsf{PK}_1\cdot u + e_1 + \textsf{M}]_{q_l}\\ \textsf{C}_2 &= [\textsf{PK}_2\cdot u + e_2]_{q_l} \nonumber \end{align} The only difference between encryption in CKKS from that in BFV is that we do not scale $\textsf{M}$ by a scalar. Note that we can encrypt and generate a ciphertext at any level $l$.

Decryption is performed by evaluating the input ciphertext in level $l$ on the secret key to generate an approximate value of the plaintext message: \begin{equation} \label{eq:decryption} \hat{\textsf{M}} = [\textsf{C}_1 + \textsf{C}_2\cdot \textsf{SK}]_{q_l} \end{equation} We leave the proof of why decryption works to the reader as an exercise. You might want to review our BFV article for some help on how to tackle this challenge.

We move now to describe how homomorphic operations are performed in CKKS. We are interested in two operations, homomorphic addition and homomorphic multiplication. The former is quite similar to that of BFV. The latter needs to be followed by rescaling to maintain the precision of computation unchanged.

Similar to BFV $\textsf{EvalAdd}$, we just add the corresponding polynomials in the input ciphertexts as shown in Equation \eqref{eq:homo:add}. Note that the input ciphertexts are assumed to be on the same level with the same scale. If that is not the case, we need to scale down the ciphertext at the higher level to match the scale and level of the other ciphertext. \begin{equation}\label{eq:homo:add} \textsf{EvalAdd}(\textsf{C}^{(1)}, \textsf{C}^{(2)}) = ([\textsf{C}^{(1)}_1 + \textsf{C}^{(2)}_1]_{q_l}, [\textsf{C}^{(1)}_2 + \textsf{C}^{(2)}_2]_{q_l}) = ( \textsf{C}^{(3)}_1, \textsf{C}^{(3)}_2) = \textsf{C}^{(3)} \end{equation}

Again, this procedure proceeds similar to $\textsf{EvalMult}$ in BFV. The derivation is also similar to what we did in BFV and we leave it to the reader as an exercise. We only show how to compute $\textsf{EvalMult}$ on two ciphertexts as follows: \begin{equation} \begin{split} \textsf{EvalMult}(C^{(1)}, C^{(2)}) = \bigg( &[\textsf{C}^{(1)}_1\cdot\textsf{C}^{(2)}_1]_{q_l}, [\textsf{C}^{(1)}_1 \cdot \textsf{C}^{(2)}_2 + \textsf{C}^{(1)}_2 \cdot \textsf{C}^{(2)}_1 ]_{q_l}, \\& [\textsf{C}^{(1)}_2 \cdot \textsf{C}^{(2)}_2]_{q_l} \bigg) = ( \textsf{C}^{(3)}_1, \textsf{C}^{(3)}_2, \textsf{C}^{(3)}_3) = \textsf{C}^{(3)} \end{split} \end{equation}

Note that $C^{(3)}$ contains 3 polynomials unlike the input ciphertexts; each containing 2 polynomials. To reduce the size of $C^{(3)}$ to 2 polynomials, we use the $\textsf{Relinearization}$ procedure which is identical to that we described in BFV except the computation should be done in $R_{q_l}$. Once we apply the relinearization procedure, we would end up with a non-expanded ciphertext (i.e., with 2 polynomials) that encrypts the product but with a squared scale factor $\Delta^2$. In fact, in CKKS, we can multiply two ciphertexts with different scale factors $\Delta_1$ and $\Delta_2$ and the product will have $ \Delta_1 \cdot \Delta_2$ as a scale factor. This is also possible in fixed-point arithmetic in the clear domain. We just need to ensure that the product fits in the datatype used to store the integer value and no wrap around (integer overflow) happens. Dealing with mixed scale factors can complicate the computation as it requires tracking of the scales. Thus, to keep the illustration simple, we stick to the case where the scale factor is fixed along the entire computation. We remark that the levels of the ciphertexts must match before we can execute $\textsf{EvalMult}$.

This procedure does not exist in the scale-invariant version of BFV we discussed in our first article. It is worth mentioning that BFV can also be instantiated as a scale-variant scheme. In that case, a procedure called $\textsf{MODSWITCH}$ can be used to switch between the ciphertext coefficient moduli. CKKS adapted the $\textsf{MODSWITCH}$ procedure and called it $\textsf{RESCALE}$. Mathematically, they are the same, but they serve two different purposes. The main purpose of using it in CKKS is typically to reduce the scale factor after multiplication to match that of the input ciphertexts. The procedure is quite simple and computationally efficient, it takes a ciphertext $\textsf{C} \in R_{q_l}^2$ and scales it down by $\Delta$ to generate an equivalent ciphertext $\hat{\textsf{C}} \in R_{q_{l-1}}^2$ encrypting the same plaintext but with reduced scale factor and reduced noise. This procedure simulates the rescaling step ($\frac{1}{2^f}$) in Equation \ref{eq:FPMul} but in the encrypted domain. \begin{equation}\label{eq:rescale} \textsf{RESCALE}(\textsf{C}, \Delta) = \frac{1}{\Delta}\cdot [\textsf{C}_1, \textsf{C}_2]_{q_l} = [\hat{\textsf{C}}]_{q_{l-1}} \end{equation}

As we said previously, CKKS simulates fixed-point arithmetic in the encrypted domain. Figures 2 and 3 can help in understanding how this can be realized. First, we study how homomorphic multiplication works in BGV. Again, we assume our ciphertext has 2 polynomials, each with a single coefficient. Also, we only focus on the polynomial that contains the payload.

Figure 2: Ciphertext multiplication in BGV. Adapted from [CKKS17].

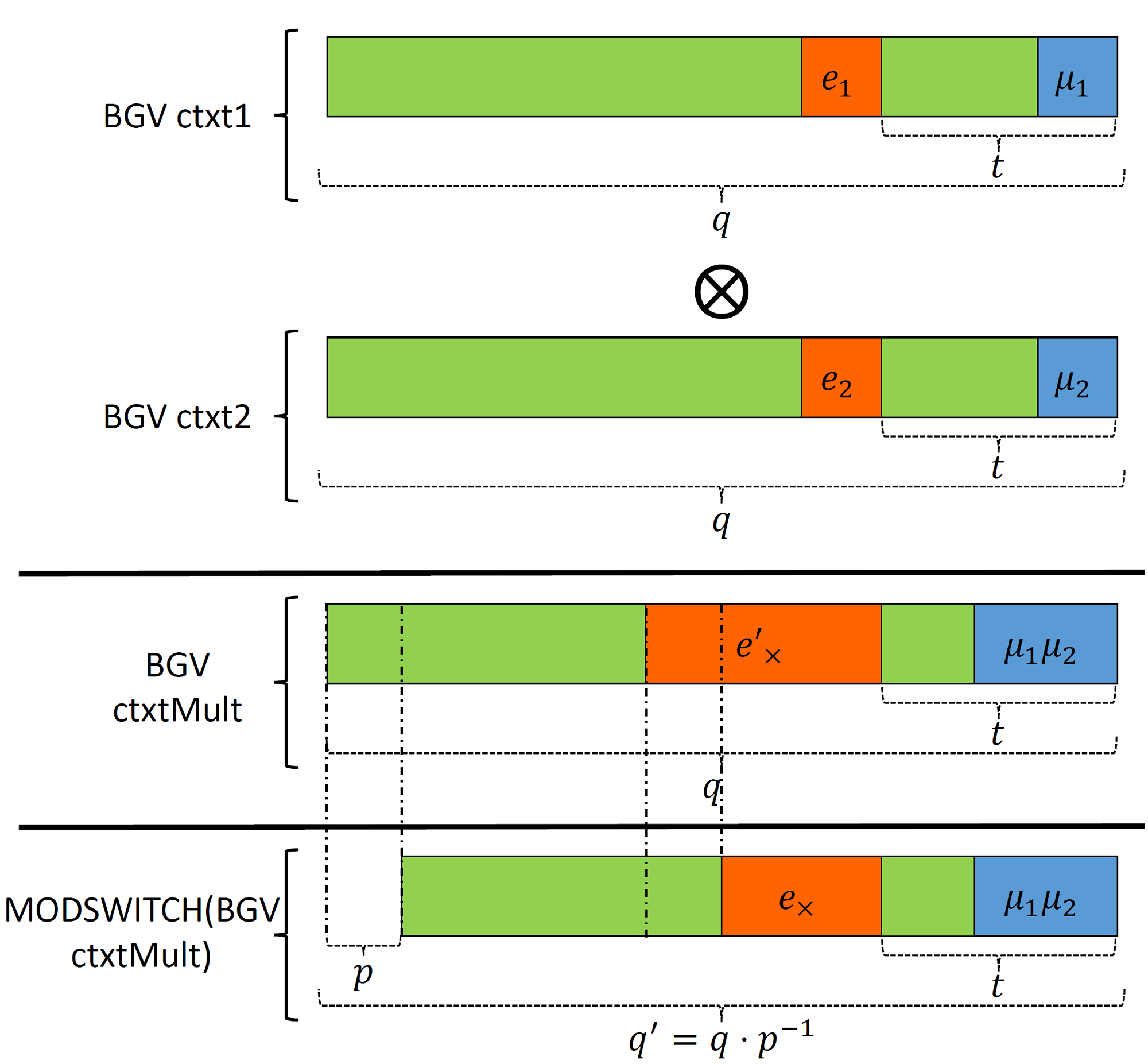
As shown in Figure 2, multiplication causes both components (payload) and noise to grow in magnitude. The multiplication result is contained within the space bounded by $t$, i.e., in the lower bits of the coefficient. The noise in the product grows similarly and takes some space from the noise budget. As mentioned previously, as long as the payload and noise are separate, decryption works successfully and the payload can be retrieved without errors. To obtain more intuition about the product ciphertext structure, let's work out the following algebraic equation: \begin{equation}\label{eq:bgv:mult:structure} \begin{split} \mu_1 \cdot \mu_2 + e'_{\times} &= (t e_1+\mu_1) \cdot (t e_2+\mu_2)\\ &= t^2 e_1 e_2 + t(e_1 \mu_2 + e_2 \mu_1) + \mu_1\mu_2 \end{split} \end{equation} To reduce the noise growth after multiplication, BGV includes a method called $\textsf{MODSWITCH}$ that takes as an input a ciphertext $\textsf{C}$ encrypting plaintext $\textsf{M}$ with coefficient modulus $q$ and returns an equivalent ciphertext $C'$ that encrypts the same plaintext but with a different coefficient modulus $q'$. Normally, $q' = \dfrac{q}{p}$ to reduce the noise, with $p$ being a number that divides $q$. Notice that this operation scales down the noise without affecting the payload component. The reason is that we choose $q'$ such that Equation \ref{eq:modswitch:constraint} is satisfied. In other words, from $t$'s perspective, $q$ and $q'$ are just the same. More concretely, we can work it out as shown in Equation \ref{eq:bgv:q:constraint}. \begin{equation}\label{eq:modswitch:constraint} q \equiv q' \mod t \end{equation} \begin{equation}\label{eq:bgv:q:constraint} \begin{split} q &\equiv q' \mod t \\ q &\equiv \frac{q}{p} \mod t \\ q &\equiv q \cdot p^{-1} \mod t \\ 1 &\equiv p^{-1} \mod t \end{split} \end{equation} From the above derivation, it is straightforward to see that multiplying by $p^{-1}$ is equivalent to multiplying by 1 modulo $t$. Therefore, the payload does not get affected by $\textsf{MODSWITCH}$ given that the constraint specified in Equation \ref{eq:modswitch:constraint} is satisfied. Note that after invoking $\textsf{MODSWITCH}$, the ciphertext moves from the level associated with $q$ to the next lower level associated with $q'$.

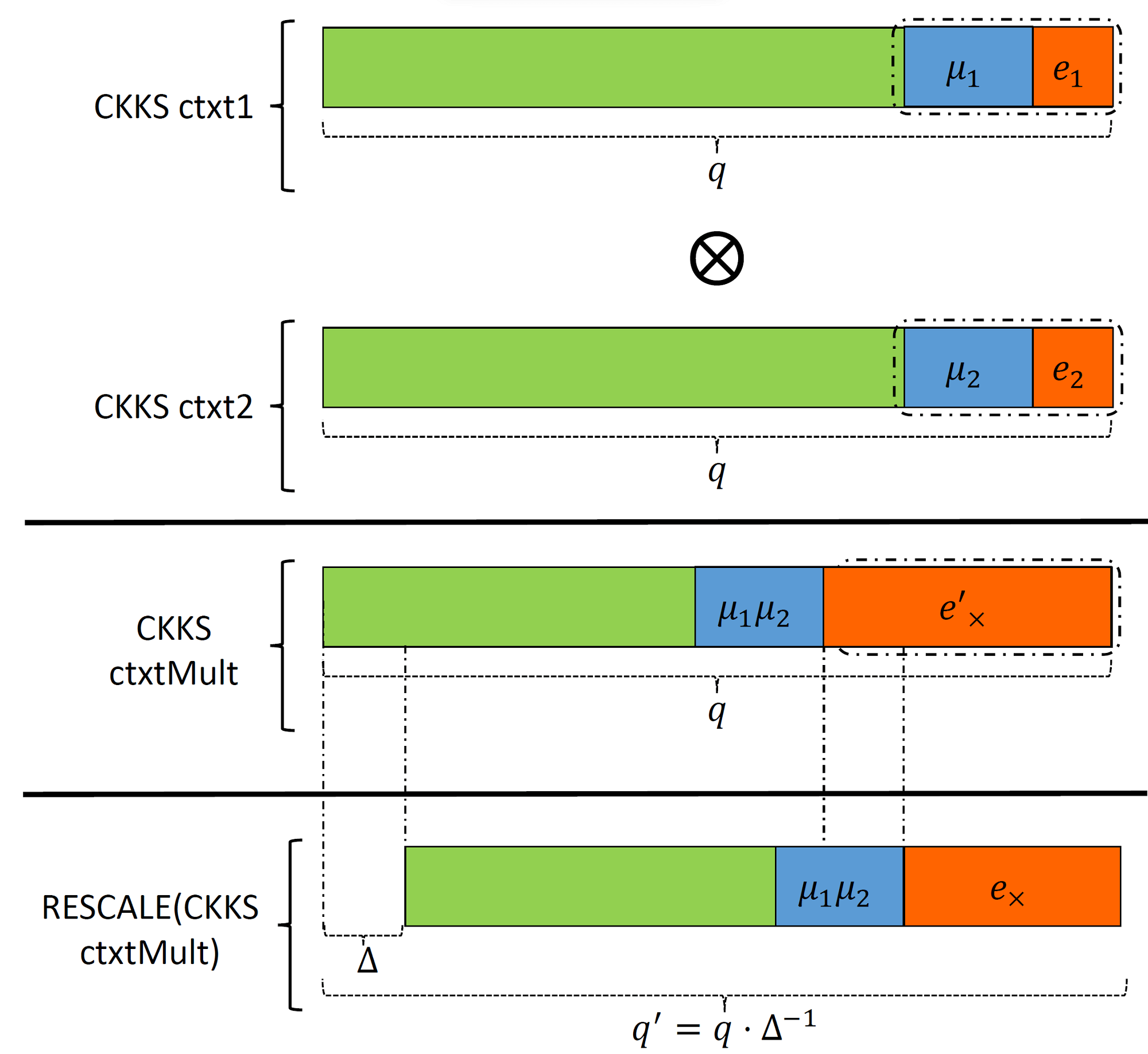
A slightly different behavior happens in CKKS. Figure 3 illustrates the inner working of CKKS homomorphic multiplication. The input plaintexts, each including payload and noise components merged as one chunk, are multiplied to generate the product of the payloads distorted by the multiplication error. We can work out Equation \ref{eq:ckks:mult:structure} similar to what we did in the BGV case. \begin{equation} \label{eq:ckks:mult:structure} \begin{split} \Delta^2 \mu_1 \cdot \mu_2 + e'_{\times} &= (\Delta \mu_1 + e_1) \cdot (\Delta \mu_2 + e_2)\\ &= \Delta^2 \mu_1 \mu_2 + \Delta(\mu_1 e_2 + \mu_2 e_1) + e_1e_2 \end{split} \end{equation} This is almost what we want except that the product payload is scaled by $\Delta^2$. To maintain the product at the same scale as the input, that is by $\Delta$, we can use $\textsf{MODSWITCH}$, which is called $\textsf{RESCALE}$ in CKKS terminology, to scale down the product by $\Delta$ and reduce the magnitude of multiplication noise. This step is similar to what we did in $\textsf{FPMul}$ \ref{eq:FPMul} to maintain the scale and precision fixed. Note that satisfying constraint \ref{eq:modswitch:constraint}, is no longer required for CKKS.

Figure 3: Ciphertext multiplication in CKKS. Adapted from [CKKS17].

As we have seen previously, CKKS includes significant similarities with other RLWE-based FHE schemes (BGV in particular). However, in terms of security, there is an important difference that was highlighted in a recent work [LM21]. An efficient passive attack was proposed against CKKS. The attack can be launched by a passive adversary (Eve) who has the following capabilities:

1. Access for an encryption oracle: this means that Eve can choose a number of messages as she wishes and ask for encrypting them to generate valid corresponding ciphertexts. This is a very reasonable assumption since FHE can be deployed as a public-key encryption scheme, that is, the encryption key is publicly available and anyone can access it. Even if FHE is deployed in secret-key mode, this is still a reasonable assumption and it forms the basis of a commonly-known attack model INDistinguishability under Chosen Plaintext (IND-CPA).
2. Ability to choose the function that would be evaluated homomorphically. This is also a reasonable assumption since Eve could be the server itself that is responsible for executing the outsourced homomorphic computation.
3. Access to a decryption oracle: this means that Eve can choose a ciphertext and ask for its decryption. This is not a very far-fetched assumption as the decryption result might be shared after computation. Some applications might require the server to know certain decrypted values (to be provided in the clear by the client after decryption) to proceed with the application.

An attack model with the aforementioned properties is now known as $\textsf{IND-CPA+}$ [LM21]. It can be seen as an attack model that is in between $\textsf{IND-CPA}$ and $\textsf{IND-CCA}$. While BFV and BGV are both secure under $\textsf{IND-CPA+}$, the vanilla CKKS is not. Without getting much into details, the attack exploits linearity in the decryption function in CKKS and the fact that approximate decryption results provide hints on the RLWE errors. Via simple algebraic manipulations, the entire secret key can be recovered in one attack attempt (in the best-case scenario). The computational requirement of this attack is finding the inverse of a polynomial in $R_q$ which can be found easily using a variant of the Extended Euclidean algorithm and Bezout's identity which can be solved in the worst-case scenario in $\mathcal{O}(n^2 \log{}n)$.

In response to this vulnerability, the attack proposers suggested tweaking the decryption function in CKKS by adding extra noise to the decryption result before publishing it to conceal the underlying RLWE noise. An open research problem is how to find tight bounds on the added noise such that CKKS is still secure under $\textsf{IND-CPA+}$ and the computational precision is not affected.

We remark that if the decryption result is never meant to be published or shared with untrusted parties, one can still use vanilla CKKS with no concerns about its security.

[ACC+18] Martin Albrecht, Melissa Chase, Hao Chen, Jintai Ding, Shafi Goldwasser, Sergey Gorbunov, Shai Halevi, Jeffrey Hoffstein, Kim Laine, Kristin Lauter, Satya Lokam, Daniele Micciancio, Dustin Moody, Travis Morrison, Amit Sahai, and Vinod Vaikuntanathan. Homomorphic encryption security standard. Technical report, HomomorphicEncryption. org, Toronto, Canada, November 2018.

[APS15] Martin R Albrecht, Rachel Player, and Sam Scott. On the concrete hardness of learning with errors. Journal of Mathematical Cryptology, 9(3):169–203, 2015.

[BGV14] Zvika Brakerski, Craig Gentry, and Vinod Vaikuntanathan. (leveled) fully homomorphic encryption without bootstrapping. ACM Transactions on Computation Theory (TOCT), 6(3):1–36, 2014.

[CH18] Hao Chen and Kyoohyung Han. Homomorphic lower digits removal and improved fhe bootstrapping. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 315–337. Springer, 2018.

[CKKS17] Jung Hee Cheon, Andrey Kim, Miran Kim, and Yongsoo Song. Homomorphic encryption for arithmetic of approximate numbers. In International Conference on the Theory and Application of Cryptology and Information Security, pages 409–437. Springer, 2017.

[CSVW16] Anamaria Costache, Nigel P Smart, Srinivas Vivek, and Adrian Waller. Fixed-point arithmetic in she schemes. In International Conference on Selected Areas in Cryptography, pages 401–422. Springer, 2016.

[FV12] Junfeng Fan and Frederik Vercauteren. Somewhat practical fully homomorphic encryption. IACR Cryptol. ePrint Arch., 2012:144, 2012.

[HS15] Shai Halevi and Victor Shoup. Bootstrapping for helib. In Annual International conference on the theory and applications of cryptographic techniques, pages 641–670. Springer, 2015.

[LM21] Baiyu Li and Daniele Micciancio. On the security of homomorphic encryption on approximate numbers. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 648–677. Springer, 2021.

Fixed-point arithmetic can be used to operate on ``finitely-precisioned'' real numbers using integer operands and operations. The basic idea is to interpret these integers to represent fractional numbers. We assume a decimal or binary point fixed (hence the name fixed-point) at a specific location in the number representation. As we operate on these integers, we keep track of the position of the point and ensure it is not affected by multiplication or division.

It is crucial to understand that fixed-point numbers represented as integers have a scaling factor that is $(>1$ or $<1)$. For instance, if we used a fixed-point number represented as integer 17 associated with a scaling factor 1/10, then what we are actually referring to is 1.7.

$Qm.f$ is a format used to describe the parameters of a fixed-point representation system, with $m$ being the number of digits used for the integral part, and $f$ being the number of digits in the fractional part. We assume signed representation (2's complement). The sign bit is usually not counted, thus in a $Q3.4$ format, our fixed-point format has 1 bit for the sign, 3 bits for the integral part ($m=3$) and 4 bits for the fractional part ($f=4$). The resolution of the fixed-point format (similar to machine epsilon in floating-point systems) is defined as $2^{-f}$. For instance, epsilon is $2^{-23}$ in IEEE-754 single-precision and $2^{-52}$ in IEEE-754 double-precision. In our $Q3.4$ format, epsilon is $2^{-4} = 0.0625$.

The dynamic range of a signed fixed-point format is bounded by $(a, a+2^{-f}, a+2^{-f}, \ldots, b-2^{-f}, b)$, where $a$ and $b$ are the minimum and maximum values supported by the format defined as follows: \begin{equation} \label{eq:Q:format:bounds} \begin{split} a &= -2^{m}\\ b &= 2^{m}-2^{-f} \end{split} \end{equation} Thus, in our $Q3.4$ format, the minimum supported number is $-2^{3} = -8$, and the maximum number is $2^{3}-2^{-4} = 8-2^{-4}$ = 7.9375, i.e., $Q3.4$ has the dynamic range $\{-8, -7.9375, \ldots, 7.9375\}$ with fixed step $2^{-4} = 0.0625$.

To convert a real number $a$ with finite-precision to a $Qm.f$ fixed-point number, simply multiply it with $2^f$ and truncate/round the fractional bits to integer. The inverse conversion can be computed by dividing the fixed-point number by $2^f$. \begin{equation} \label{eq:conv:real:to:fixed} \begin{split} \textsf{R2FP}(a) &= \textsf{RoundToInt or Truncate}(a\cdot2^f)\\ \textsf{FP2R}(a) &= \dfrac{a}{2^f} \end{split} \end{equation}

Adding two fixed-point numbers is easy given that their scale is the same. \begin{equation} \label{eq:FPAdd} \textsf{FPAdd} (a_1, a_2) = a_1 + a_2 \end{equation} Subtraction works similarly as shown below. Note that neither addition nor subtraction changes the scale factor, or they do not change the place of the decimal/binary point. \begin{equation} \label{eq:FPSub} \textsf{FPSub} (a_1, a_2) = a_1 - a_2 \end{equation}

Multiplication is a bit trickier than addition as it results in changing the result's scale factor. Remember that we use a fixed-point format in which the position of the decimal/binary point is fixed. Therefore, multiplication is typically followed by rescaling to make the scaling factor of the result unchanged. Assuming the scaling factors of the inputs are identical, multiplication can be calculated as follows: \begin{equation} \label{eq:FPMul} \textsf{FPMul} (a_1, a_2) = (a_1 * a_2) / 2^f \end{equation} Division can be calculated similarly but we multiply by the scale factor as follows: \begin{equation} \label{eq:FPDiv} \textsf{FPDiv} (a_1, a_2) = (a_1 / a_2) * 2^f \end{equation}

We provide below an example of how to perform fixed-point arithmetic in $Q15.16$. The example was generated using $\texttt{C++}$. The real values of $a$ and $b$ are defined using the datatype $\texttt{float}$. The output precision was set to 9 using the command cout.precision(std::numeric_limits<float>::max_digits10). For each operation, we show 3 outputs;

1. fixed-point result of the fixed-point operation,
2. converted result from fixed-point to $\texttt{float}$
3. the result as performed using IEEE-754 single-precision operations which can be used to serve as ground truth.

As we can see, the calculated results in fixed-point arithmetic are slightly less accurate compared to IEEE-754 single-precision operations. Our sample code and its output are provided below for reference.

#include <iostream>
#include <math.h>
#include <limits>

using namespace std;

const int f = 16;
const int scaleFactor = (1 << f);
typedef std::numeric_limits<float> flt;

#define FloatToFixed(x) (x * (float)scaleFactor)
#define FixedToFloat(x) ((float)x / (float)scaleFactor)

#define Add(x, y) (x+y)
#define Sub(x, y) (x-y)
#define Mul(x,y) ((int64_t)((int64_t)x*y)/scaleFactor)
#define Div(x,y) ((int64_t)((int64_t)x*scaleFactor)/y)

int
main ()
{
    cout.precision(flt::max_digits10);

    float float_a = 1.3, float_b = 2.7;
  
    int fixed_a = FloatToFixed (float_a);
    int fixed_b = FloatToFixed (float_b);
  
    int fixedAdd = Add(fixed_a, fixed_b);
    int fixedSub = Sub(fixed_a, fixed_b);
    int fixedMul = Mul(fixed_a, fixed_b);
    int fixedDiv = Div(fixed_a, fixed_b);

    cout << "Output precision = " << flt::max_digits10 << " decimal digits\n";
    cout << "scale factor = (2^" << f << " = " << scaleFactor << ")" << endl << endl;
    cout << "a (float) = " << float_a << endl;
    cout << "b (float) = " << float_b << endl << endl;
  
    cout << "a (fixed): " << fixed_a << endl;
    cout << "b (fixed): " << fixed_b << endl;

    cout << "\nfixed add (fixed): " << fixedAdd << endl;    
    cout << "fixed add (float): " << FixedToFloat(fixedAdd) << endl;
    cout << "float add (float): " << float_a+float_b << endl;
  
    cout << "\nfixed sub (fixed): " << fixedSub << endl;
    cout << "fixed sub (float): " << FixedToFloat(fixedSub) << endl;
    cout << "float sub (float): " << float_a-float_b << endl;
  
    cout << "\nfixed mul (fixed): " << fixedMul << endl;
    cout << "fixed mul (float): " << FixedToFloat(fixedMul) << endl;
    cout << "float mul (float): " << float_a*float_b << endl;
  
    cout << "\nfixed div (fixed): " << fixedDiv << endl;
    cout << "fixed div (float): " << FixedToFloat(fixedDiv) << endl;
    cout << "float div (float): " << float_a/float_b << endl;

    return 0;
}